User guide¶
This section includes the machine/trainer guides for learning techniques available in this package.
Machines¶
Machines are one of the core components of Bob. They represent statistical models or other functions defined by parameters that can be learnt or set by using Trainers.
K-means machines¶
k-means is a clustering
method which aims to partition a set of observations into 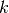 clusters.
The training procedure is described further below. Here, we explain only how
to use the resulting machine. For the sake of example, we create a new
clusters.
The training procedure is described further below. Here, we explain only how
to use the resulting machine. For the sake of example, we create a new
bob.learn.em.KMeansMachine as follows:
>>> machine = bob.learn.em.KMeansMachine(2,3) # Two clusters with a feature dimensionality of 3
>>> machine.means = numpy.array([[1,0,0],[0,0,1]], 'float64') # Defines the two clusters
Then, given some input data, it is possible to determine to which cluster the data is the closest as well as the min distance.
>>> sample = numpy.array([2,1,-2], 'float64')
>>> print(machine.get_closest_mean(sample)) # Returns the index of the closest mean and the distance to it at the power of 2
(0, 6.0)
Gaussian machines¶
The bob.learn.em.Gaussian represents a multivariate diagonal
Gaussian (or normal) distribution. In this
context, a diagonal Gaussian refers to the covariance matrix of the
distribution being diagonal. When the covariance matrix is diagonal, each
variable in the distribution is independent of the others.
Objects of this class are normally used as building blocks for more complex
bob.learn.em.GMMMachine or GMM objects, but can also be used
individually. Here is how to create one multivariate diagonal Gaussian
distribution:
>>> g = bob.learn.em.Gaussian(2) #bi-variate diagonal normal distribution
>>> g.mean = numpy.array([0.3, 0.7], 'float64')
>>> g.mean
array([ 0.3, 0.7])
>>> g.variance = numpy.array([0.2, 0.1], 'float64')
>>> g.variance
array([ 0.2, 0.1])
Once the bob.learn.em.Gaussian has been set, you can use it to
estimate the log-likelihood of an input feature vector with a matching number
of dimensions:
>>> log_likelihood = g(numpy.array([0.4, 0.4], 'float64'))
As with other machines you can save and re-load machines of this type using
bob.learn.em.Gaussian.save() and the class constructor
respectively.
Gaussian mixture models¶
The bob.learn.em.GMMMachine represents a Gaussian mixture model (GMM), which consists of a
mixture of weighted bob.learn.em.Gaussians.
>>> gmm = bob.learn.em.GMMMachine(2,3) # Mixture of two diagonal Gaussian of dimension 3
By default, the diagonal Gaussian distributions of the GMM are initialized with
zero mean and unit variance, and the weights are identical. This can be updated
using the bob.learn.em.GMMMachine.means,
bob.learn.em.GMMMachine.variances or
bob.learn.em.GMMMachine.weights.
>>> gmm.weights = numpy.array([0.4, 0.6], 'float64')
>>> gmm.means = numpy.array([[1, 6, 2], [4, 3, 2]], 'float64')
>>> gmm.variances = numpy.array([[1, 2, 1], [2, 1, 2]], 'float64')
>>> gmm.means
array([[ 1., 6., 2.],
[ 4., 3., 2.]])
Once the bob.learn.em.GMMMachine has been set, you can use it to
estimate the log-likelihood of an input feature vector with a matching number
of dimensions:
>>> log_likelihood = gmm(numpy.array([5.1, 4.7, -4.9], 'float64'))
As with other machines you can save and re-load machines of this type using
bob.learn.em.GMMMachine.save() and the class constructor respectively.
Gaussian mixture models Statistics¶
The bob.learn.em.GMMStats is a container for the sufficient
statistics of a GMM distribution.
Given a GMM, the sufficient statistics of a sample can be computed as follows:
>>> gs = bob.learn.em.GMMStats(2,3)
>>> sample = numpy.array([0.5, 4.5, 1.5])
>>> gmm.acc_statistics(sample, gs)
>>> print(gs)
Then, the sufficient statistics can be accessed (or set as below), by considering the following attributes.
>>> gs = bob.learn.em.GMMStats(2,3)
>>> log_likelihood = -3. # log-likelihood of the accumulated samples
>>> T = 1 # Number of samples used to accumulate statistics
>>> n = numpy.array([0.4, 0.6], 'float64') # zeroth order stats
>>> sumpx = numpy.array([[1., 2., 3.], [4., 5., 6.]], 'float64') # first order stats
>>> sumpxx = numpy.array([[10., 20., 30.], [40., 50., 60.]], 'float64') # second order stats
>>> gs.log_likelihood = log_likelihood
>>> gs.t = T
>>> gs.n = n
>>> gs.sum_px = sumpx
>>> gs.sum_pxx = sumpxx
Joint Factor Analysis¶
Joint Factor Analysis (JFA) [1] [2] is a session variability modelling
technique built on top of the Gaussian mixture modelling approach. It utilises
a within-class subspace 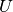 , a between-class subspace
, a between-class subspace 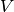 , and a
subspace for the residuals
, and a
subspace for the residuals 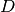 to capture and suppress a significant
portion of between-class variation.
to capture and suppress a significant
portion of between-class variation.
An instance of bob.learn.em.JFABase carries information about
the matrices 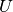 ,
, 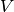 and
and 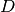 , which can be shared between
several classes. In contrast, after the enrollment phase, an instance of
, which can be shared between
several classes. In contrast, after the enrollment phase, an instance of
bob.learn.em.JFAMachine carries class-specific information about
the latent variables 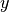 and
and  .
.
An instance of bob.learn.em.JFABase can be initialized as
follows, given an existing GMM:
>>> jfa_base = bob.learn.em.JFABase(gmm,2,2) # dimensions of U and V are both equal to 2
>>> U = numpy.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10], [11, 12]], 'float64')
>>> V = numpy.array([[6, 5], [4, 3], [2, 1], [1, 2], [3, 4], [5, 6]], 'float64')
>>> d = numpy.array([0, 1, 0, 1, 0, 1], 'float64')
>>> jfa_base.u = U
>>> jfa_base.v = V
>>> jfa_base.d = d
Next, this bob.learn.em.JFABase can be shared by several
instances of bob.learn.em.JFAMachine, the initialization being
as follows:
>>> m = bob.learn.em.JFAMachine(jfa_base)
>>> m.y = numpy.array([1,2], 'float64')
>>> m.z = numpy.array([3,4,1,2,0,1], 'float64')
Once the bob.learn.em.JFAMachine has been configured for a
specific class, the log-likelihood (score) that an input sample belongs to the
enrolled class, can be estimated, by first computing the GMM sufficient
statistics of this input sample, and then calling the
bob.learn.em.JFAMachine.log_likelihood() on the sufficient statistics.
>>> gs = bob.learn.em.GMMStats(2,3)
>>> gmm.acc_statistics(sample, gs)
>>> score = m(gs)
As with other machines you can save and re-load machines of this type using
bob.learn.em.JFAMachine.save() and the class constructor
respectively.
Inter-Session Variability¶
Similarly to Joint Factor Analysis, Inter-Session Variability (ISV) modelling
[3] [2] is another session variability modelling technique built on top of
the Gaussian mixture modelling approach. It utilises a within-class subspace
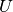 and a subspace for the residuals
and a subspace for the residuals 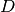 to capture and suppress a
significant portion of between-class variation. The main difference compared to
JFA is the absence of the between-class subspace
to capture and suppress a
significant portion of between-class variation. The main difference compared to
JFA is the absence of the between-class subspace 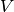 .
.
Similarly to JFA, an instance of bob.learn.em.JFABase carries
information about the matrices 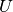 and
and 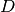 , which can be shared
between several classes, whereas an instance of
, which can be shared
between several classes, whereas an instance of
bob.learn.em.JFAMachine carries class-specific information about
the latent variable  .
.
An instance of bob.learn.em.ISVBase can be initialized as
follows, given an existing GMM:
>>> isv_base = bob.learn.em.ISVBase(gmm,2) # dimension of U is equal to 2
>>> isv_base.u = U
>>> isv_base.d = d
Next, this bob.learn.em.ISVBase can be shared by several
instances of bob.learn.em.ISVMachine, the initialization being
as follows:
>>> m = bob.learn.em.ISVMachine(isv_base)
>>> m.z = numpy.array([3,4,1,2,0,1], 'float64')
Once the bob.learn.em.ISVMachine has been configured for a
specific class, the log-likelihood (score) that an input sample belongs to the
enrolled class, can be estimated, by first computing the GMM sufficient
statistics of this input sample, and then calling the
__call__ on the sufficient statistics.
>>> gs = bob.learn.em.GMMStats(2,3)
>>> gmm.acc_statistics(sample, gs)
>>> score = m(gs)
As with other machines you can save and re-load machines of this type using
bob.learn.em.ISVMachine.save() and the class constructor
respectively.
Total Variability (i-vectors)¶
Total Variability (TV) modelling [4] is a front-end initially introduced for
speaker recognition, which aims at describing samples by vectors of low
dimensionality called i-vectors. The model consists of a subspace 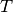 and a residual diagonal covariance matrix
and a residual diagonal covariance matrix 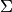 , that are then used to
extract i-vectors, and is built upon the GMM approach.
, that are then used to
extract i-vectors, and is built upon the GMM approach.
An instance of the class bob.learn.em.IVectorMachine carries
information about these two matrices. This can be initialized as follows:
>>> m = bob.learn.em.IVectorMachine(gmm, 2)
>>> m.t = numpy.array([[1.,2],[4,1],[0,3],[5,8],[7,10],[11,1]])
>>> m.sigma = numpy.array([1.,2.,1.,3.,2.,4.])
Once the bob.learn.em.IVectorMachine has been set, the
extraction of an i-vector 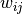 can be done in two steps, by first
extracting the GMM sufficient statistics, and then estimating the i-vector:
can be done in two steps, by first
extracting the GMM sufficient statistics, and then estimating the i-vector:
>>> gs = bob.learn.em.GMMStats(2,3)
>>> gmm.acc_statistics(sample, gs)
>>> w_ij = m(gs)
As with other machines you can save and re-load machines of this type using
bob.learn.em.IVectorMachine.save() and the class constructor
respectively.
Probabilistic Linear Discriminant Analysis (PLDA)¶
Probabilistic Linear Discriminant Analysis [5] [6] is a probabilistic model
that incorporates components describing both between-class and within-class
variations. Given a mean 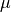 , between-class and within-class subspaces
, between-class and within-class subspaces
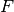 and
and 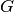 and residual noise
and residual noise  with zero mean and
diagonal covariance matrix
with zero mean and
diagonal covariance matrix 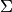 , the model assumes that a sample
, the model assumes that a sample
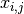 is generated by the following process:
is generated by the following process:
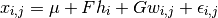
Information about a PLDA model (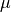 ,
, 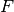 ,
, 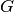 and
and
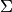 ) are carried out by an instance of the class
) are carried out by an instance of the class
bob.learn.em.PLDABase.
>>> ### This creates a PLDABase container for input feature of dimensionality 3,
>>> ### and with subspaces F and G of rank 1 and 2 respectively.
>>> pldabase = bob.learn.em.PLDABase(3,1,2)
Class-specific information (usually from enrollment samples) are contained in
an instance of bob.learn.em.PLDAMachine, that must be attached
to a given bob.learn.em.PLDABase. Once done, log-likelihood
computations can be performed.
>>> plda = bob.learn.em.PLDAMachine(pldabase)
>>> samples = numpy.array([[3.5,-3.4,102], [4.5,-4.3,56]], dtype=numpy.float64)
>>> loglike = plda.compute_log_likelihood(samples)
Trainers¶
In the previous section, the concept of a machine was introduced. A machine is fed by some input data, processes it and returns an output. Machines can be learnt using trainers in Bob.
Expectation Maximization¶
Each one of the following trainers has their own initialize, eStep and mStep methods in order to train the respective machines. For example, to train a K-Means with 10 iterations you can use the following steps.
>>> data = numpy.array([[3,-3,100], [4,-4,98], [3.5,-3.5,99], [-7,7,-100], [-5,5,-101]], dtype='float64') #Data
>>> kmeans_machine = bob.learn.em.KMeansMachine(2, 3) # Create a machine with k=2 clusters with a dimensionality equal to 3
>>> kmeans_trainer = bob.learn.em.KMeansTrainer() #Creating the k-means machine
>>> max_iterations = 10
>>> kmeans_trainer.initialize(kmeans_machine, data) #Initilizing the means with random values
>>> for i in range(max_iterations):
... kmeans_trainer.e_step(kmeans_machine, data)
... kmeans_trainer.m_step(kmeans_machine, data)
>>> print(kmeans_machine.means)
[[ -6. 6. -100.5]
[ 3.5 -3.5 99. ]]
With that granularity you can train your K-Means (or any trainer procedure) with your own convergence criteria.
Furthermore, to make the things even simpler, it is possible to train the K-Means (and have the same example as above) using the wrapper bob.learn.em.train as in the example below:
>>> data = numpy.array([[3,-3,100], [4,-4,98], [3.5,-3.5,99], [-7,7,-100], [-5,5,-101]], dtype='float64') #Data
>>> kmeans_machine = bob.learn.em.KMeansMachine(2, 3) # Create a machine with k=2 clusters with a dimensionality equal to 3
>>> kmeans_trainer = bob.learn.em.KMeansTrainer() #Creating the k-means machine
>>> max_iterations = 10
>>> bob.learn.em.train(kmeans_trainer, kmeans_machine, data, max_iterations = 10) #wrapper for the em trainer
>>> print(kmeans_machine.means)
[[ -6. 6. -100.5]
[ 3.5 -3.5 99. ]]
K-means¶
k-means [7] is a clustering method, which aims to partition a set of
observations into 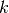 clusters. This is an unsupervised technique. As
for PCA [1], which is implemented in the
clusters. This is an unsupervised technique. As
for PCA [1], which is implemented in the bob.learn.linear.PCATrainer
class, the training data is passed in a 2D numpy.ndarray container.
>>> data = numpy.array([[3,-3,100], [4,-4,98], [3.5,-3.5,99], [-7,7,-100], [-5,5,-101]], dtype='float64')
The training procedure will learn the means for the
bob.learn.em.KMeansMachine. The number 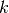 of means is given
when creating the machine, as well as the dimensionality of the features.
of means is given
when creating the machine, as well as the dimensionality of the features.
>>> kmeans = bob.learn.em.KMeansMachine(2, 3) # Create a machine with k=2 clusters with a dimensionality equal to 3
Then training procedure for k-means is an Expectation-Maximization-based [8] algorithm. There are several options that can be set such as the maximum number of iterations and the criterion used to determine if the convergence has occurred. After setting all of these options, the training procedure can then be called.
>>> kmeansTrainer = bob.learn.em.KMeansTrainer()
>>> bob.learn.em.train(kmeansTrainer, kmeans, data, max_iterations = 200, convergence_threshold = 1e-5) # Train the KMeansMachine
>>> print(kmeans.means)
[[ -6. 6. -100.5]
[ 3.5 -3.5 99. ]]
Maximum likelihood for Gaussian mixture model¶
A Gaussian mixture model (GMM) [9] is a common probabilistic model. In
order to train the parameters of such a model it is common to use a
maximum-likelihood (ML) approach [10]. To do this we use an
Expectation-Maximization (EM) algorithm [8]. Let’s first start by creating
a bob.learn.em.GMMMachine. By default, all of the Gaussian’s have
zero-mean and unit variance, and all the weights are equal. As a starting
point, we could set the mean to the one obtained with k-means [7].
>>> gmm = bob.learn.em.GMMMachine(2,3) # Create a machine with 2 Gaussian and feature dimensionality 3
>>> gmm.means = kmeans.means # Set the means to the one obtained with k-means
The Bob class to learn the parameters of a GMM [9] using ML [10] is
bob.learn.em.ML_GMMTrainer. It uses an EM-based [8] algorithm
and requires the user to specify which parameters of the GMM are updated at
each iteration (means, variances and/or weights). In addition, and as for
k-means [7], it has parameters such as the maximum number of iterations
and the criterion used to determine if the parameters have converged.
>>> trainer = bob.learn.em.ML_GMMTrainer(True, True, True) # update means/variances/weights at each iteration
>>> bob.learn.em.train(trainer, gmm, data, max_iterations = 200, convergence_threshold = 1e-5)
>>> print(gmm)
MAP-adaptation for Gaussian mixture model¶
Bob also supports the training of GMMs [9] using a maximum a posteriori (MAP) approach [11]. MAP is closely related to the ML [10] technique but it incorporates a prior on the quantity that we want to estimate. In our case, this prior is a GMM [9]. Based on this prior model and some training data, a new model, the MAP estimate, will be adapted.
Let’s consider that the previously trained GMM [9] is our prior model.
>>> print(gmm)
The training data used to compute the MAP estimate [11] is again stored in a
2D numpy.ndarray container.
>>> dataMAP = numpy.array([[7,-7,102], [6,-6,103], [-3.5,3.5,-97]], dtype='float64')
The Bob class used to perform MAP adaptation training [11] is
bob.learn.em.MAP_GMMTrainer. As with the ML estimate [10], it uses
an EM-based [8] algorithm and requires the user to specify which parts of
the GMM are adapted at each iteration (means, variances and/or weights). In
addition, it also has parameters such as the maximum number of iterations and
the criterion used to determine if the parameters have converged, in addition
to this there is also a relevance factor which indicates the importance we give
to the prior. Once the trainer has been created, a prior GMM [9] needs to be
set.
>>> relevance_factor = 4.
>>> trainer = bob.learn.em.MAP_GMMTrainer(gmm, relevance_factor=relevance_factor, update_means=True, update_variances=False, update_weights=False) # mean adaptation only
>>> gmmAdapted = bob.learn.em.GMMMachine(2,3) # Create a new machine for the MAP estimate
>>> bob.learn.em.train(trainer, gmmAdapted, dataMAP, max_iterations = 200, convergence_threshold = 1e-5)
>>> print(gmmAdapted)
Joint Factor Analysis¶
The training of the subspace 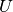 ,
, 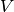 and
and 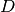 of a Joint
Factor Analysis model, is performed in two steps. First, GMM sufficient
statistics of the training samples should be computed against the UBM GMM. Once
done, we get a training set of GMM statistics:
of a Joint
Factor Analysis model, is performed in two steps. First, GMM sufficient
statistics of the training samples should be computed against the UBM GMM. Once
done, we get a training set of GMM statistics:
>>> F1 = numpy.array( [0.3833, 0.4516, 0.6173, 0.2277, 0.5755, 0.8044, 0.5301, 0.9861, 0.2751, 0.0300, 0.2486, 0.5357]).reshape((6,2))
>>> F2 = numpy.array( [0.0871, 0.6838, 0.8021, 0.7837, 0.9891, 0.5341, 0.0669, 0.8854, 0.9394, 0.8990, 0.0182, 0.6259]).reshape((6,2))
>>> F=[F1, F2]
>>> N1 = numpy.array([0.1379, 0.1821, 0.2178, 0.0418]).reshape((2,2))
>>> N2 = numpy.array([0.1069, 0.9397, 0.6164, 0.3545]).reshape((2,2))
>>> N=[N1, N2]
>>> gs11 = bob.learn.em.GMMStats(2,3)
>>> gs11.n = N1[:,0]
>>> gs11.sum_px = F1[:,0].reshape(2,3)
>>> gs12 = bob.learn.em.GMMStats(2,3)
>>> gs12.n = N1[:,1]
>>> gs12.sum_px = F1[:,1].reshape(2,3)
>>> gs21 = bob.learn.em.GMMStats(2,3)
>>> gs21.n = N2[:,0]
>>> gs21.sum_px = F2[:,0].reshape(2,3)
>>> gs22 = bob.learn.em.GMMStats(2,3)
>>> gs22.n = N2[:,1]
>>> gs22.sum_px = F2[:,1].reshape(2,3)
>>> TRAINING_STATS = [[gs11, gs12], [gs21, gs22]]
In the following, we will allocate a bob.learn.em.JFABase machine,
that will then be trained.
>>> jfa_base = bob.learn.em.JFABase(gmm, 2, 2) # the dimensions of U and V are both equal to 2
Next, we initialize a trainer, which is an instance of
bob.learn.em.JFATrainer, as follows:
>>> jfa_trainer = bob.learn.em.JFATrainer()
The training process is started by calling the
bob.learn.em.train().
>>> bob.learn.em.train_jfa(jfa_trainer, jfa_base, TRAINING_STATS, max_iterations=10)
Once the training is finished (i.e. the subspaces 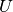 ,
, 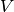 and
and
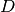 are estimated), the JFA model can be shared and used by several
class-specific models. As for the training samples, we first need to extract
GMM statistics from the samples. These GMM statistics are manually defined in
the following.
are estimated), the JFA model can be shared and used by several
class-specific models. As for the training samples, we first need to extract
GMM statistics from the samples. These GMM statistics are manually defined in
the following.
>>> Ne = numpy.array([0.1579, 0.9245, 0.1323, 0.2458]).reshape((2,2))
>>> Fe = numpy.array([0.1579, 0.1925, 0.3242, 0.1234, 0.2354, 0.2734, 0.2514, 0.5874, 0.3345, 0.2463, 0.4789, 0.5236]).reshape((6,2))
>>> gse1 = bob.learn.em.GMMStats(2,3)
>>> gse1.n = Ne[:,0]
>>> gse1.sum_px = Fe[:,0].reshape(2,3)
>>> gse2 = bob.learn.em.GMMStats(2,3)
>>> gse2.n = Ne[:,1]
>>> gse2.sum_px = Fe[:,1].reshape(2,3)
>>> gse = [gse1, gse2]
Class-specific enrollment can then be perfomed as follows. This will estimate
the class-specific latent variables 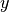 and
and  :
:
>>> m = bob.learn.em.JFAMachine(jfa_base)
>>> jfa_trainer.enroll(m, gse, 5) # where 5 is the number of enrollment iterations
More information about the training process can be found in [12] and [13].
Inter-Session Variability¶
The training of the subspace 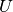 and
and 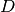 of an Inter-Session
Variability model, is performed in two steps. As for JFA, GMM sufficient
statistics of the training samples should be computed against the UBM GMM. Once
done, we get a training set of GMM statistics. Next, we will allocate an
of an Inter-Session
Variability model, is performed in two steps. As for JFA, GMM sufficient
statistics of the training samples should be computed against the UBM GMM. Once
done, we get a training set of GMM statistics. Next, we will allocate an
bob.learn.em.ISVBase machine, that will then be trained.
>>> isv_base = bob.learn.em.ISVBase(gmm, 2) # the dimensions of U is equal to 2
Next, we initialize a trainer, which is an instance of
bob.learn.em.ISVTrainer, as follows:
>>> isv_trainer = bob.learn.em.ISVTrainer(relevance_factor=4.) # 4 is the relevance factor
The training process is started by calling the
bob.learn.em.train().
>>> bob.learn.em.train(isv_trainer, isv_base, TRAINING_STATS, max_iterations=10)
Once the training is finished (i.e. the subspaces 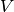 and
and 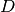 are
estimated), the ISV model can be shared and used by several class-specific
models. As for the training samples, we first need to extract GMM statistics
from the samples. Class-specific enrollment can then be perfomed, which will
estimate the class-specific latent variable
are
estimated), the ISV model can be shared and used by several class-specific
models. As for the training samples, we first need to extract GMM statistics
from the samples. Class-specific enrollment can then be perfomed, which will
estimate the class-specific latent variable  :
:
>>> m = bob.learn.em.ISVMachine(isv_base)
>>> isv_trainer.enroll(m, gse, 5) # where 5 is the number of iterations
More information about the training process can be found in [14] and [13].
Total Variability (i-vectors)¶
The training of the subspace 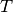 and
and 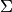 of a Total
Variability model, is performed in two steps. As for JFA and ISV, GMM
sufficient statistics of the training samples should be computed against the
UBM GMM. Once done, we get a training set of GMM statistics. Next, we will
allocate an instance of
of a Total
Variability model, is performed in two steps. As for JFA and ISV, GMM
sufficient statistics of the training samples should be computed against the
UBM GMM. Once done, we get a training set of GMM statistics. Next, we will
allocate an instance of bob.learn.em.IVectorMachine, that will
then be trained.
>>> m = bob.learn.em.IVectorMachine(gmm, 2)
>>> m.variance_threshold = 1e-5
Next, we initialize a trainer, which is an instance of
bob.learn.em.IVectorTrainer, as follows:
>>> ivec_trainer = bob.learn.em.IVectorTrainer(update_sigma=True)
>>> TRAINING_STATS_flatten = [gs11, gs12, gs21, gs22]
The training process is started by calling the
bob.learn.em.train().
>>> bob.learn.em.train(ivec_trainer, m, TRAINING_STATS_flatten, max_iterations=10)
More information about the training process can be found in [15].
Probabilistic Linear Discriminant Analysis (PLDA)¶
Probabilistic Linear Discriminant Analysis [16] is a probabilistic model that
incorporates components describing both between-class and within-class
variations. Given a mean 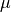 , between-class and within-class subspaces
, between-class and within-class subspaces
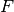 and
and 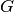 and residual noise
and residual noise  with zero mean and
diagonal covariance matrix
with zero mean and
diagonal covariance matrix 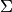 , the model assumes that a sample
, the model assumes that a sample
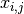 is generated by the following process:
is generated by the following process:
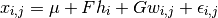
An Expectaction-Maximization algorithm can be used to learn the parameters of
this model 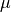 ,
, 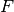
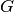 and
and 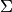 . As these
parameters can be shared between classes, there is a specific container class
for this purpose, which is
. As these
parameters can be shared between classes, there is a specific container class
for this purpose, which is bob.learn.em.PLDABase. The process is
described in detail in [17].
Let us consider a training set of two classes, each with 3 samples of dimensionality 3.
>>> data1 = numpy.array([[3,-3,100], [4,-4,50], [40,-40,150]], dtype=numpy.float64)
>>> data2 = numpy.array([[3,6,-50], [4,8,-100], [40,79,-800]], dtype=numpy.float64)
>>> data = [data1,data2]
Learning a PLDA model can be performed by instantiating the class
bob.learn.em.PLDATrainer, and calling the
bob.learn.em.train() method.
>>> ### This creates a PLDABase container for input feature of dimensionality 3,
>>> ### and with subspaces F and G of rank 1 and 2 respectively.
>>> pldabase = bob.learn.em.PLDABase(3,1,2)
>>> trainer = bob.learn.em.PLDATrainer()
>>> bob.learn.em.train(trainer, pldabase, data, max_iterations=10)
Once trained, this PLDA model can be used to compute the log-likelihood of a
set of samples given some hypothesis. For this purpose, a
bob.learn.em.PLDAMachine should be instantiated. Then, the
log-likelihood that a set of samples share the same latent identity variable
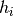 (i.e. the samples are coming from the same identity/class) is
obtained by calling the
(i.e. the samples are coming from the same identity/class) is
obtained by calling the
bob.learn.em.PLDAMachine.compute_log_likelihood() method.
>>> plda = bob.learn.em.PLDAMachine(pldabase)
>>> samples = numpy.array([[3.5,-3.4,102], [4.5,-4.3,56]], dtype=numpy.float64)
>>> loglike = plda.compute_log_likelihood(samples)
If separate models for different classes need to be enrolled, each of them with
a set of enrolment samples, then, several instances of
bob.learn.em.PLDAMachine need to be created and enrolled using
the bob.learn.em.PLDATrainer.enroll() method as follows.
>>> plda1 = bob.learn.em.PLDAMachine(pldabase)
>>> samples1 = numpy.array([[3.5,-3.4,102], [4.5,-4.3,56]], dtype=numpy.float64)
>>> trainer.enroll(plda1, samples1)
>>> plda2 = bob.learn.em.PLDAMachine(pldabase)
>>> samples2 = numpy.array([[3.5,7,-49], [4.5,8.9,-99]], dtype=numpy.float64)
>>> trainer.enroll(plda2, samples2)
Afterwards, the joint log-likelihood of the enrollment samples and of one or several test samples can be computed as previously described, and this separately for each model.
>>> sample = numpy.array([3.2,-3.3,58], dtype=numpy.float64)
>>> l1 = plda1.compute_log_likelihood(sample)
>>> l2 = plda2.compute_log_likelihood(sample)
In a verification scenario, there are two possible hypotheses: 1.
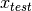 and
and 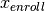 share the same class. 2.
share the same class. 2.
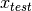 and
and 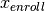 are from different classes. Using the
methods
are from different classes. Using the
methods bob.learn.em.PLDAMachine.log_likelihood_ratio() or
its alias __call__ function, the corresponding
log-likelihood ratio will be computed, which is defined in more formal way by:
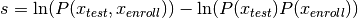
>>> s1 = plda1(sample)
>>> s2 = plda2(sample)
| [1] | (1, 2) http://dx.doi.org/10.1109/TASL.2006.881693 |
| [2] | (1, 2) http://publications.idiap.ch/index.php/publications/show/2606 |
| [3] | http://dx.doi.org/10.1016/j.csl.2007.05.003 |
| [4] | http://dx.doi.org/10.1109/TASL.2010.2064307 |
| [5] | http://dx.doi.org/10.1109/ICCV.2007.4409052 |
| [6] | http://doi.ieeecomputersociety.org/10.1109/TPAMI.2013.38 |
| [7] | (1, 2, 3) http://en.wikipedia.org/wiki/K-means_clustering |
| [8] | (1, 2, 3, 4) http://en.wikipedia.org/wiki/Expectation-maximization_algorithm |
| [9] | (1, 2, 3, 4, 5, 6) http://en.wikipedia.org/wiki/Mixture_model |
| [10] | (1, 2, 3, 4) http://en.wikipedia.org/wiki/Maximum_likelihood |
| [11] | (1, 2, 3) http://en.wikipedia.org/wiki/Maximum_a_posteriori_estimation |
| [12] | http://dx.doi.org/10.1109/TASL.2006.881693 |
| [13] | (1, 2) http://publications.idiap.ch/index.php/publications/show/2606 |
| [14] | http://dx.doi.org/10.1016/j.csl.2007.05.003 |
| [15] | http://dx.doi.org/10.1109/TASL.2010.2064307 |
| [16] | http://dx.doi.org/10.1109/ICCV.2007.4409052 |
| [17] | http://doi.ieeecomputersociety.org/10.1109/TPAMI.2013.38 |
